
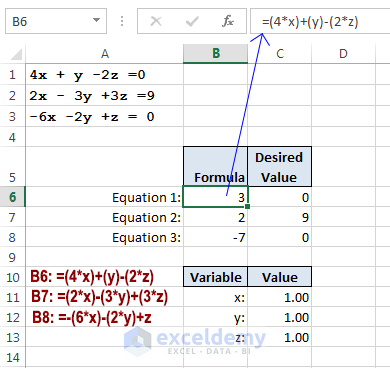
Variable bounds: Decision variables are rarely allowed to take on any value (from minus infinity to plus infinity).Constraints: These are mathematical functions that incorporate decision variables to express boundaries on possible solutions.
A manager's goal is to either maximise or minimise the objective function. Objective function: This is a math-ematical function that incorporates decision variables to express a manager's goals.The goal, then, is to determine those values that maximise or minimise the objective function.
These variables usually represent identifiable "things" or inputs that a manager can control (ie, how many of each specific model of washing machines to produce).
MS EXCEL SOLVER FUNCTION FREE
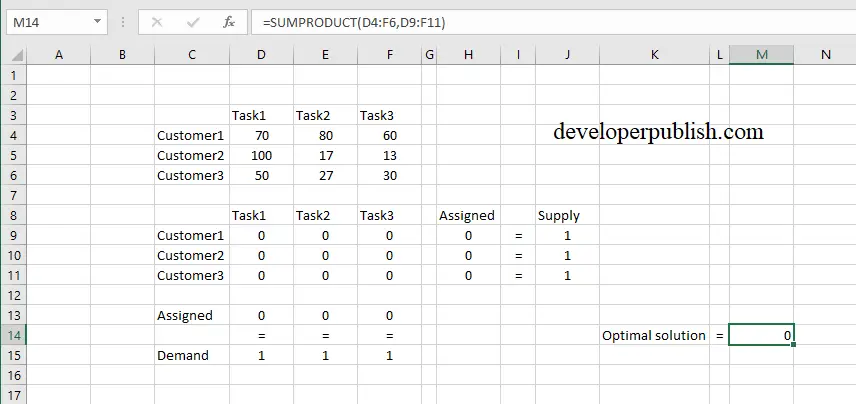
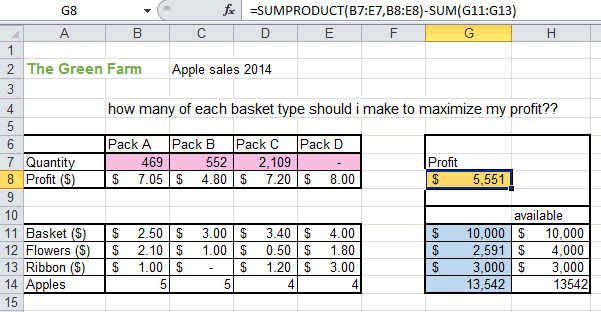
This article provides a description of linear programming, demonstrates how it can be performed using Microsoft Excel's free Solver add-in, and illustrates its use through an example from management accounting. Linear programming is one technique that accountants can often readily apply to determine the best outcome in these situations. It is therefore important that they apply appropriate analytical techniques in approaching such decisions. Many of these decisions require management accountants to determine or recommend specific courses of action that would lead to an optimal outcome (such as maximising profits or minimising costs) given a limited set of resources (such as production inputs). A management accountant's knowledge of relevant revenues and costs is important for many decisions, among them capital budgeting, outsourcing, special orders, product mix, and the adding or dropping of specific product lines.


 0 kommentar(er)
0 kommentar(er)
